Black- Scholes option pricing model explanation

 Black- Scholes option pricing model

1) Model Usage:

The Black-Scholes model is a mathematical model specifically used to price financial derivatives of European options, and can be abbreviated as the BS formula. The BS formula can be used by investors to estimate the theoretical value of option products using the market price as a reference in the formula. In addition, the BS formula can be used by option issuers to calculate the initial price of options.

2) Model Form

European Call Option BS Formula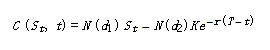

European Put Option BS formula

“CSt.t” and “PSt.” represent the European call option price and European put option price. “St” represents the price of the underlying asset at the moment, “K” the contract price, “T” the expiration date of the option, and “r” the risk-free interest rate (generally replaced by the Treasury yield and interbank offered rate. “ ” represents the volatility of the underlying asset, and “t” stands for the current moment.


“d1” and “d2” are the model parameters and the expressions are as follows:

3) Greek alphabet based on the BS formula

The BS formula provides a mathematical objective value for European options. And each of the partial derivatives of the option values can also be calculated through the BS formula for each parameter, i.e., the analytical expressions of the Greek coefficients of the European option can be obtained through the BS by the following chart: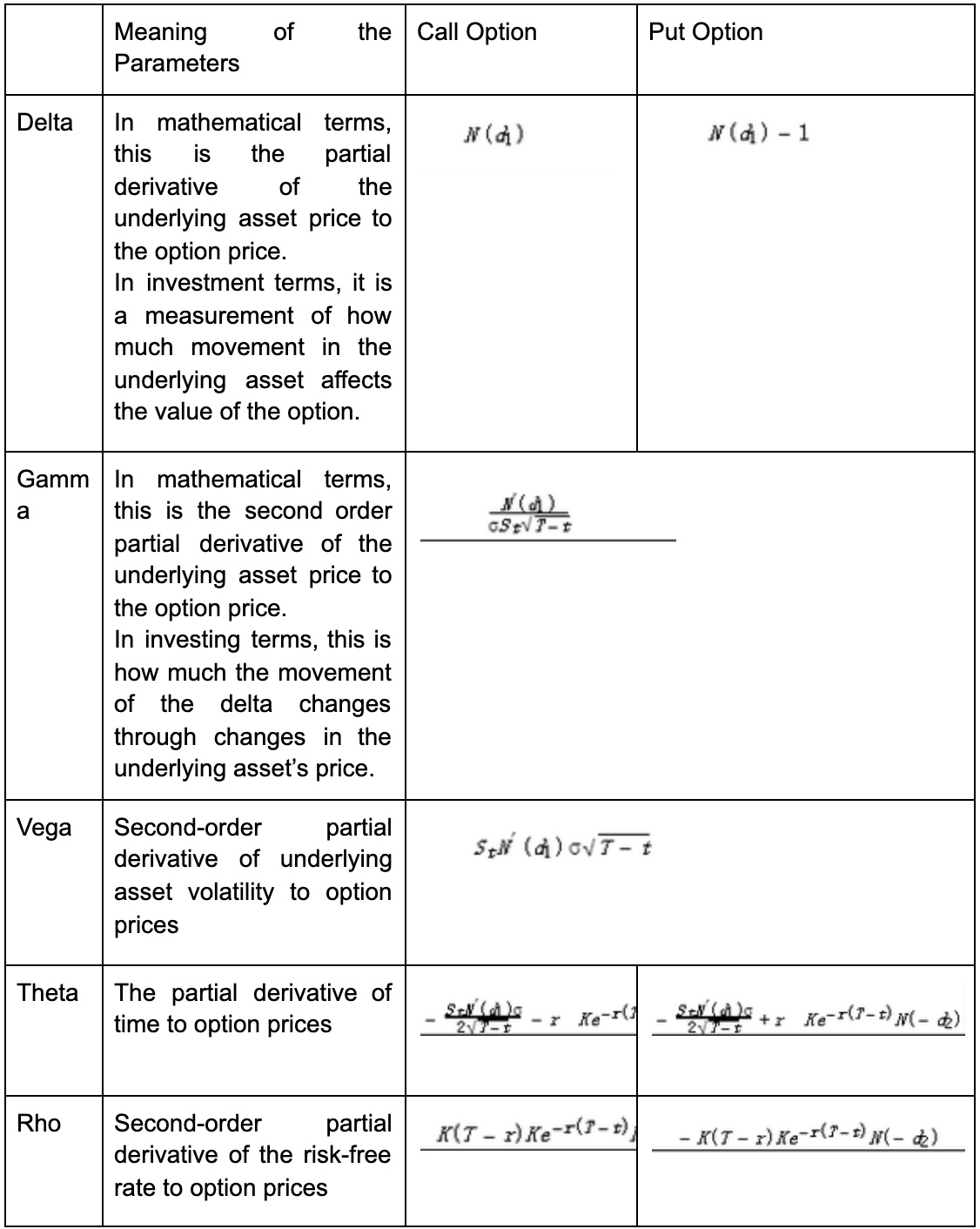

“N” represents the function of probability density in the univariate normal distribution. The relationship between the European option price change and the parameters can be analyzed. The Delta coefficient of a European call option is always greater than zero, and the price of a European call option increases as the price of the underlying asset increases. The Delta coefficient of the European put option is always less than zero, and the price of the European put option decreases as the price of the underlying asset increases.

4) In the Black-Sholes model, put option price decreases as the underlying asset increases.

The Gamma coefficient and Vega coefficient of both the European put option and the call option are greater than zero. It indicates that the value of the European option increases as the volatility level of the underlying asset increases. The Rho coefficient of the European call option is greater than or equal to zero, while the Rho coefficient of the European put option is less than or equal to zero. This means that the price of the European option increases with the risk-free rate, while the price of the European put option decreases with it.



5) Limitations of the Black-Scholes Model
The Black-Scholes model has two major limitations. First, the BlackSchole model can only be used for single-asset financial product prices for European-style options, and cannot be used to price U.S. options, Asian options, and multi-asset options: Second, the effectiveness of the BackScholes model depends heavily on the model assumptions such as a normal probability distribution. When the model assumptions are invalid or partially invalid, the prices determined by the Black-Scholes model are inaccurate.


The Black-Scholes model requires that the price of the underlying asset is a random variable that is independently and identically distributed. There is no regular correlation to other inputs. The Black-Scholes model also requires that the volatility and risk-free rate are fixed and free of heteroskedasticity and time-varying characteristics. In the digital currency trading market, the assumptions relied on by the Black-Scholes model are difficult to satisfy. In general, there is significant heterogeneity in the probability distribution of digital currency prices at different times. There is prominent heteroskedasticity and serial correlation. In pricing derivatives with digital currencies as the underlying asset, adjustments to the Black-Scholes model are needed, such as replacing Brownian motion with Levy processes, and fixed volatility with stochastic volatility models, moving average, and GARCH models.


When using the Levy process and stochastic volatility model to improve the Black-Scholes model, it is usually impossible to obtain the option price expression in analytical form. It is necessary to use the numerical solution to obtain the option price, which is more difficult for the investors. Investors are recommended to use the moving average and GARCH to improve Black-Scholes model. By doing so, the time-varying option price in the Black-Scholes pricing model can be obtained. The moving average volatility is relatively easy to calculate: just to introduce MA function into the volatility. Investors can use R language, Python inner functions, and the underlying digital currency returns to calculate the time-varying volatility in the GARCH model.